Find the length of the curve x = cos² t. y = sin² t. 0 ≤ts T. O O O O O O O TT™ TT 4√2 S- S 2√2 Write the definite inte

[answerhappygod]

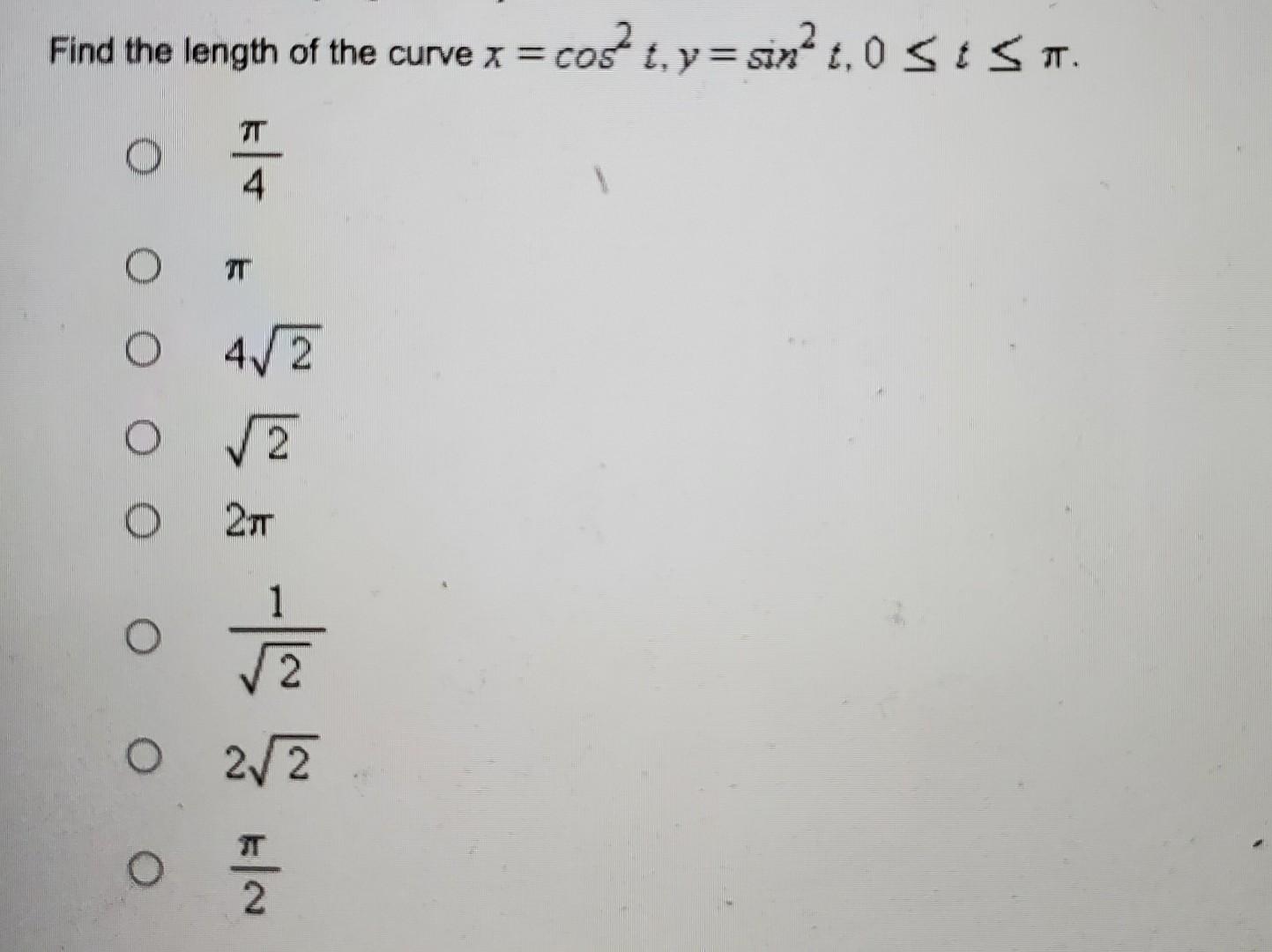
Find The Length Of The Curve X Cos T Y Sin T 0 Ts T O O O O O O O Tt Tt 4 2 S S 2 2 Write The Definite Inte 1 (83.69 KiB) Viewed 8 times

Find The Length Of The Curve X Cos T Y Sin T 0 Ts T O O O O O O O Tt Tt 4 2 S S 2 2 Write The Definite Inte 2 (130.98 KiB) Viewed 8 times

Find The Length Of The Curve X Cos T Y Sin T 0 Ts T O O O O O O O Tt Tt 4 2 S S 2 2 Write The Definite Inte 3 (123.86 KiB) Viewed 8 times

Find the length of the curve x = cos² t. y = sin² t. 0 ≤ts T. O O O O O O O TT™ TT 4√2 S- S 2√2
Write the definite integral representing the length of the curve with parametric equations, y=g(t), a ≤t ≤ b. b [1 + ƒ' (t)]² dt O a 'O b √1 + [f^{²}]}² d R b [2mtf(1) R b ju(1) + + g'(t)}² d a } 0 √ √(1) ³²³ + 8²(1) ² dt Q dź j=v(³ & a j√₁ Q / 1 + [g'(t)]² dt b © J(1 O + [f'(t)]²) dt
Find the length of the curve y = ln (cos x), 0 ≤ x ≤ 4 O 1- O O oo O in√2-1 √2-1 2 1 금 2 √2-1 금 in(1+√2) in O ○ 2-2 O √2